박 세용 
최근 인공지능이 적용된 검색 엔진은 우리가 상상하는 것보다 훨씬 복잡한 과정을 거쳐 정보를 찾아줍니다. “에베레스트 산의 높이는 얼마인가요?”라는 단순한 질문 뒤에는 인터넷에 흩어진 수십억 개의 문서, 이미지, 영상 중에서 가장 관련성 높은 정보를 찾아내는 정교한 기술이 숨어 있습니다. 오늘은 최근 검색 엔진 기술 트렌드를 이해하는데 뺄 수 없는 임베딩 기술과 벡터 검색 그리고 다중 벡터 활용에 대해 이야기하려고 합니다. 이 글은 최근 구글 리서치에서 발표한 논문, MUVERA: Making multi-vector retrieval as fast as single-vector search (https://research.google/blog/muvera-making-multi-vector-retrieval-as-fast-as-single-vector-search/) 을 읽고 저 같은 비 개발자도 이해할 수 있는 수준으로 관련 내용을 찾아 최대한 쉽게 풀어서 정리한 것입니다.
검색에 사용되는 임베딩 기술
이러한 정보 검색의 핵심에는 임베딩(embedding) 기술이 자리 잡고 있습니다. 임베딩은 텍스트, 이미지, 음성 등 다양한 형태의 데이터를 컴퓨터가 이해할 수 있는 숫자 배열, 즉 벡터로 변환하는 기술입니다. 이때 비슷한 의미를 가진 데이터들은 서로 유사한 벡터 값을 갖게 되는데, 이렇게 되는 이유는 사람이 작성한 대량의 문서를 학습한 인공지능이 이들 단어를 임베딩 처리를 할 때 ‘비슷한 의미’를 가진 데이터들을 실제로 서로 가까운, 유사한 벡터 값을 갖지도록 하기 때문입니다. 예를 들어 “고양이”와 “강아지”는 둘 다 반려동물이고, “귀엽다”, “애완동물” 같은 비슷한 문맥에서 자주 함께 등장합니다. 인공지능은 이런 문맥 정보를 활용해서, “고양이”와 “강아지”를 숫자 공간에서 서로 가깝게 위치하도록 벡터 값을 정하게 됩니다. 반대로, “고양이”와 “자동차”처럼 전혀 관련 없는 단어들은 멀리 떨어진 벡터로 만들어집니다.
이런 방식은 텍스트뿐만 아니라 이미지, 소리 등 다양한 데이터에도 똑같이 적용됩니다. 예를 들어, “호수 풍경”과 “바다 풍경” 이미지의 임베딩 벡터는 서로 가깝고, “호수 풍경”과 “자동차 경주” 이미지는 서로 멀리 떨어지게 검색에 이용되는 인공지능을 학습시킵니다.
결국, 임베딩 모델이 수많은 데이터를 보면서, “비슷한 건 가깝게, 다른 건 멀게” 벡터 공간에 자동으로 배치하는 것이고, 이렇게 해서 임베딩 벡터는 단순한 숫자 배열이 아니라, 의미의 비슷함과 다름을 반영하는 일종의 ‘의미 지도’를 만드는 일을 합니다. 심지어 “암시된 분위기”나 “은유, 반어, 유머” 같은 미묘한 차이
까지도 학습 데이터 안에서 패턴을 찾아냅니다.
예를 들어 “이 영화, 생각보다 재밌네?”, “이 영화, 생각보다 재미없네.”와 같은 이 두 문장은 단어 몇 개만 다르지만, 임베딩 모델은 이 두문장의 전체 문맥, 뉘앙스(긍정/부정)를 반영해서 서로 다른 벡터로 분류할 수 있습니다.
“이곳은 정말 시원하다.”와 “이곳은 정말 시원하다(비꼼, 냉랭한 분위기에서)”와 같이 분리가 쉬워보이지 않는 두 문장의 뉘앙스 차이도, 임베딩 모델이 읽어낸 데이터(다양한 문맥과 예시)가 많을 수록 더 잘 구분할 수 있습니다. 물론 현재까지는 완벽하진 않습니다. 하지만, 분명 점점 더 좋아지고 있습니다. 그래서 검색에서 “비슷한 느낌, 유사한 문장” 찾기, 추천에서 “문맥상 어울리는 콘텐츠” 찾기 등이 가능해집니다. 이렇게 임베딩 모델이 만들어낸 벡터 데이터는 단순한 숫자 배열이 아니라, 서로 비슷한 의미를 가진 데이터끼리 가까이, 전혀 다른 의미를 가진 데이터끼리는 멀리 떨어져 위치하게 되는 ‘의미 지도’ 의 역할을 하게 됩니다.
문맥, 뉘앙스, 심지어 암시된 분위기까지 반영된 이 벡터들을 활용하면, 이제 우리는 데이터 간의 ‘비슷함’과 ‘다름’을 아주 직관적으로 다룰 수 있게 됩니다. 그렇다면, 임베딩 수십억 개의 벡터들 중에서 “내 질문에 가장 비슷한 답을 가진 데이터”를 찾아내려면 어떻게 해야 할까요? 여기서 바로 내적(dot product) 연산이 중요한 역할을 하게 됩니다. 내적(dot product) 같은 간단한 수학적 연산으로 데이터 간의 유사도를 파악하는 것입니다. 여기서 말하는 내적은 쉽게 말해, 두 벡터가 얼마나 비슷한 방향을 바라보고 있는 지를 수치로 나타내 주는 계산입니다.
내적 계산의 예시:
벡터 A = (2, 3, 5), 벡터 B = (4, 1, 7)
두 벡터의 내적의 계산 : A · B = (2×4) + (3×1) + (5×7) = 8 + 3 + 35= 46
이 값이 클수록 두 벡터, 즉 두 데이터는 서로 더 비슷한 의미를 가진 것이라고 볼 수 있습니다. 반대로, 내적 값이 작거나 0에 가깝다면 서로 거의 관련이 없는 의미라는 뜻입니다. 일반적으로 크고 작고의 기준을 정할 수 없기 때문에 벡터값을 정규화해서 숫자 1에 가까우면(즉, 두 벡터의 방향이 같으면) 큰것이고, 숫자 0에 가까우면(즉, 두 벡터의 방향이 90도에 가까우면) 작은 것이다. 그래서 유사도를 내적의 크기를 가지고도 이야기를 하지만 두 벡터의 코사인 값(cosθ=(A · B)/(|A| × |B|) , 1 ~ -1)을 가지고도 유사도를 표현하기도 합니다.
이러한 내적 계산의 이용은 매우 단순하면서도 컴퓨터가 아주 빠르게 처리할 수 있기 때문에, 수십억 개의 데이터 중에서 내 질문(쿼리)과 가장 비슷한 벡터를 거의 실시간으로 찾는데 도움이 됩니다. 그래서 최근의 인공지능 검색 엔진이나 추천 시스템은 가장 유사한 결과를 신속하게 찾아주는 데 임베딩 벡터만들어 놓은 후에 이를 기반으로 내적 연산을 이용하는 것입니다.
전통적인 단일 벡터 방식의 문제 해결을 위한 다중 벡터의 활용
구글이 2018년에 BERT를 발표한 이후로 지금까지 대부분의 검색 시스템은 단일 벡터(single-vector) 방식인 듀얼 인코더 모델(RankEmbed 등)을 사용해왔습니다. 이는 하나의 문서나 쿼리를 하나의 고정된 크기 벡터로 표현하는 방식입니다. 예를 들어, “인공지능의 발전과 미래 전망”이라는 긴 문서를 512차원의 하나의 벡터로 압축하는 것입니다. 하지만 이 방식에는 근본적인 한계가 있습니다. 복잡하고 다양한 내용을 담고 있는 문서를 하나의 벡터로 요약하다 보면, 문서 내부의 세밀한 의미나 뉘앙스들이 손실될 수밖에 없습니다. 마치 교향곡 전체를 한 음으로 표현하려는 것과 같은 무리가 따릅니다.
이런 한계를 극복하기 위해 등장한 것이 2020년 스탠포드 대학에서 제시한 ColBERT(Contexualized Late Interaction over BERT) 모델로 문서의 각 단어나 토큰(token)마다 별도의 벡터를 생성하는 다중 벡터(multi-vector) 모델입니다. 예를 들어, “파리는 프랑스의 수도입니다”라는 문장에서 “파리”, “프랑스”, “수도”라는 단어 각각에 대해 개별적인 벡터를 만드는 것입니다. 이렇게 하면 문서 내의 각 개념이 가진 고유한 의미와 맥락을 보다 정확하게 포착할 수 있습니다. 다중 벡터 모델은 분명히 더 정확한 검색 결과를 제공합니다. 하지만 이런 정확성에는 큰 대가가 따릅니다. 바로 계산 복잡도와 비용이 폭발적 증가합니다.
단일 벡터 방식에서는 쿼리 벡터 하나와 문서 벡터 하나만 비교하면 되지만 다중 벡터 방식에서는 쿼리의 모든 토큰 벡터를 문서의 모든 토큰 벡터와 비교해야 합니다. 만약 쿼리에 50개의 단어가 있고 문서에도 50개의 단어가 있다면, 총 2,500번의 비교 연산이 필요합니다.
다중 벡터 간의 유사도를 계산을 위해 쿼리 토큰에 대해 가장 유사한 문서 토큰을 찾고, 반대로 각 문서 토큰에 대해 가장 유사한 쿼리 토큰을 찾는 샴퍼 유사도(Chamfer similarity)의 복잡한 계산 과정은 수백만, 수천만 개의 문서가 있는 실제 검색 환경에서는 계산 시간과 비용이 감당하기 어려운 수준으로 증가한다는 큰 문제를 동반합니다.
이런 기존 다중 벡터 유사도도 분석 방식의 문제를 해결하기 위해 등장한 최신 검색/임베딩 변환 알고리즘이 구글 리서치 팀의 “MUVERA: Multi-Vector Retrieval via Fixed Dimensional Encodings” 논문에 소개된 MUVERA(무베라)입니다. 무베라의 핵심 아이디어는 다중 벡터를 다시 고정 차원 인코딩 (Fixed Dimensional Encoding, FDE)이라는 방법으로 하나의 벡터로 변환하는 것입니다. 복잡한 오케스트라 연주를 하나의 대표 선율로 요약하되, 원곡의 본질적 특성은 그대로 유지하는 것이라 말할 수 있습니다. 여러 개의 벡터가 담고 있는 풍부한 의미 정보를 최대한 보존하면서도, 계산 효율성을 위해 하나의 벡터로 압축하는 것입니다.
무베라의 또 다른 혁신은 복잡한 다중 벡터 유사도 계산 문제를 최대 내적 검색(Maximum Inner Product Search, MIPS) 문제로 변환한다는 점입니다. 이를 간단하게 말하면 많은 벡터가 저장된 데이터베이스에서 내가 던진 검색 쿼리의 벡터와 내적이 값이 가장 큰 벡터를 빠르게 찾아 내주는 기술입니다. MIPS라는 분야는 이미 잘 연구되어 있는 최적화 검색 알고리즘들이 많이 존재하는 영역입니다. 즉, 무베라는 “다중 벡터 계산이라는 새로운 어려운 문제”를 “이미 잘 해결된 기존 문제”로 바꿔주는 역할을 하는 새로운 접근법이라 할 수 있습니다.
이 알고리즘은 기존의 다중 벡터 모델이 가진 느린 검색 속도, 높은 메모리 사용량, 확장성의 한계를 크게 개선하여, 웹 검색뿐만 아니라 유튜브 같은 추천 시스템, 자연어 처리 등 다양한 분야에서 활용될 수 있습니다. 무베라의 가장 큰 혁신은 고정 차원 인코딩(FDE)이라는 방식을 통해, 다중 벡터 정보를 하나의 고정된 벡터로 효율적으로 압축하면서도 의미 정보를 최대한 보존한다는 점입니다. 다중 벡터 모델의 높은 정확도를 유지하면서도, 단일 벡터 방식 수준의 빠른 검색 속도와 낮은 메모리 사용량, 뛰어난 확장성을 제공합니다.
이 방식은 기존 듀얼 인코더 모델인 RankEmbed(구글 검색에서 사용되는 대표적인 듀얼 인코더 기반 임베딩 모델)모델이 일반적인 쿼리에는 빠르고 효율적이지만, 드문 질의(테일 쿼리)에는 약한 문제까지 보완합니다. 실제로 무베라는 웹 스케일 환경에서도 기존 검색 시스템에 쉽게 도입할 수 있고, 다양한 분야에 걸쳐 정확도와 효율성을 모두 향상시킬 수 있는 차세대 다중 벡터 검색 기술로 평가받고 있습니다.
무베라의 작동 메카니즘
1단계: 고정 차원 인코딩 생성
무베라의 첫 번째 단계는 쿼리와 문서의 다중 벡터를 각각 하나의 FDE( Fixed Dimensional Encoding, 고정 차원 인코딩)로 변환합니다. 이 과정에서 사용되는 변환 함수는 데이터 독립적(data-agnostic, 즉, 어떤 주제, 어떤 문서, 어떤 포맷, 어떤 언어 이든 똑같은 규칙으로 변환 한다는 의미)입니다. 즉, 어떤 종류의 데이터가 들어와도 일관되게 적용될 수 있는 범용적인 방법입니다.
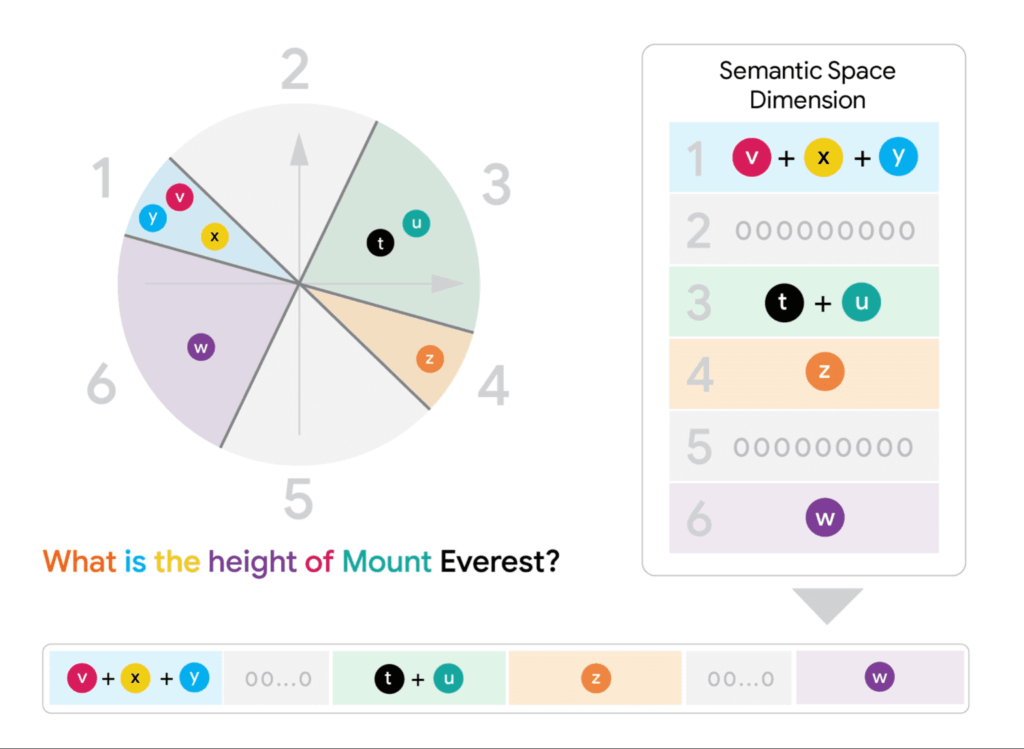
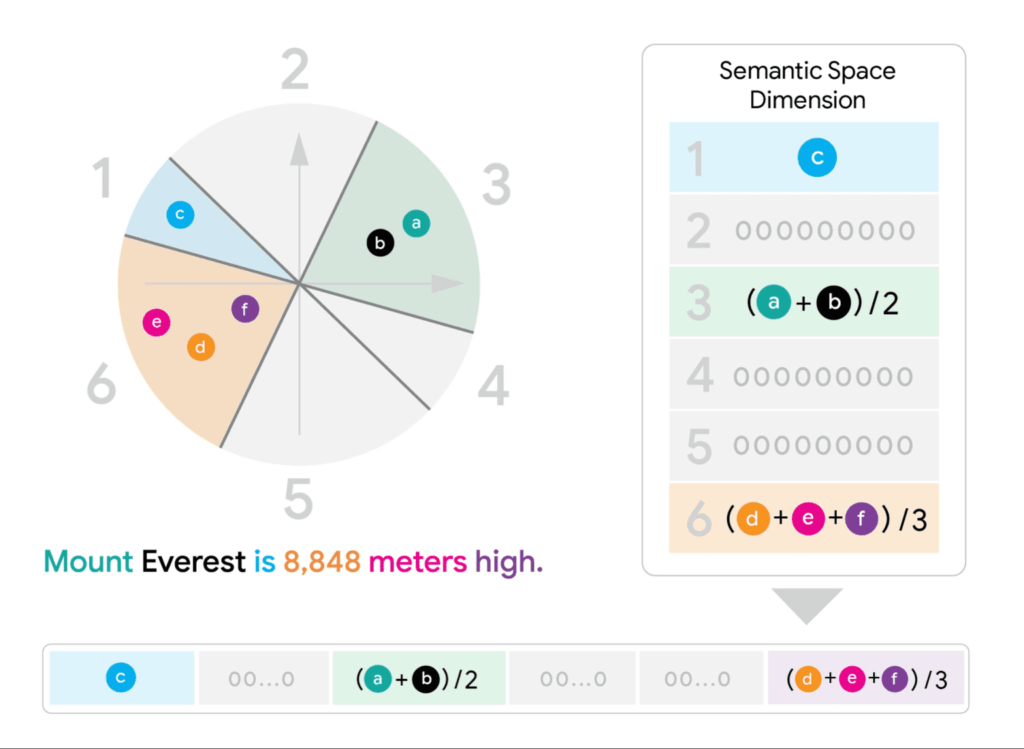
예를 들어, 50개 토큰으로 구성된 문서가 있다면, 각 토큰의 벡터들을 특정 규칙에 따라 조합하여 하나의 대표 벡터를 만들어냅니다. 이때 원본 다중 벡터들이 가지고 있던 의미적 정보를 최대한 보존하도록 설계됩니다.
예시:
문장 “고양이는 귀엽다”를 임베딩한다고 생각해봅시다.
- “고양이” → [0.2, 0.8, 0.1]
- “는” → [0.1, 0.1, 0.1]
- “귀엽다” → [0.7, 0.2, 0.9]
이렇게 단어(토큰)별로 3차원 벡터가 있다고 할 때 이를 FDE(고정 차원 인코딩)로 합치면, 아래와 같이 변환 할 수 있습니다.
- “고양이” + “는” + “귀엽다” =
[0.2+0.1+0.7, 0.8+0.1+0.2, 0.1+0.1+0.9]
= [1.0, 1.1, 1.1]
이렇게 하면, 원래 3개의 벡터(각 3차원) → 합쳐서 1개의 3차원 벡터가 됩니다. 실제 무베라의 FDE는 훨씬 더 정교한 합산/조합 방법을 쓰지만, “여러 개의 벡터 → 하나의 고정된 벡터”로 합치는 기본 원리는 이 예시와 비슷하게 처리됩니다.
2단계: 효율적인 후보 검색
생성된 FDE들을 사용하여 근사 최근접 이웃 검색(Approximate Nearest Neighbor Search, ANN)을 수행합니다. 이는 “내가 던진 쿼리 벡터와 가장 비슷한(가장 가까운) 벡터들”을 완벽하게(정확히) 찾는 대신, ‘거의 비슷하게’(근사적으로) 빠르게 찾아주는 기술입니다. 왜냐하면 데이터가 수백만~수십억 개로 많을 때, 모두 일일이 비교하면 너무 느려지기 때문입니다. 그래서 “99% 맞으면 된다”는 생각으로, 정확성은 조금 양보하고, 속도를 대폭 올리는 방식입니다.
이 단계에서는 기존의 최적화된 인덱싱 기술들을 그대로 활용할 수 있습니다. “비슷한 벡터끼리는 같은 ‘버킷’(상자)으로 보내주는 해싱(분류) 방법”으로 공간을 여러 구역(버킷)으로 나누고, 전체를 전수 비교하지 않고, 쿼리 벡터가 들어있는 버킷에 저장된 벡터들만 비교하는 라이브러리인 LSH(Locality Sensitive Hashing), 페이스북이 만든 “벡터 데이터의 빠른 근사 검색”을 위한 오픈소스 라이브러리로서 LSH를 포함한 다양한 고속 인덱싱 기법, GPU 가속, 대용량 데이터 지원 등 벡터 검색 분야의 표준처럼 쓰이고 있는 FAISS(Facebook AI Similarity Search), 그리고 구글에서 만든, “대규모 임베딩 벡터의 빠른 근사 최근접 이웃 검색” 라이브러리로 효율성과 메모리 사용량을 더 개선한 구조를 갖고 있어, 구글 내부/외부 서비스에서 대규모로 사용되는 ScaNN(Scalable Nearest Neighbors) 등 이미 검증된 고속 검색 라이브러리들을 바로 활용합니다.
3단계: 정밀 재순위화
마지막 단계에서는 2단계에서 선별된 후보 문서들에 대해 원본 다중 벡터를 사용한 정밀한 유사도 계산을 수행합니다. 이때 샴퍼 유사도 같은 복잡한 계산 방법을 사용하지만, 대상이 소수의 후보 문서들로 제한되어 있기 때문에 전체적인 계산 비용은 합리적인 수준으로 유지됩니다.
무베라가 의미를 가지는 가장 중요한 수학적 근거는 근사 보존(approximation preservation)이라는 원리 때문입니다. 근사 보존은 “복잡한 원래 계산”을 “더 단순한 계산”으로 바꿔도, 결과가 거의 똑같거나 일정한 오차 내에서 보장된다는 수학적 원리입니다. 여기서는 즉, FDE를 사용한 유사도 계산 결과가 원본 다중 벡터를 사용한 계산 결과와 수학적으로 근사한다는 것입니다. 이는 단순한 경험적 관찰이 아니라 이론적으로 증명된 특성입니다. 무베라 논문에서는 특정 조건 하에서 이런 근사 보장이 성립함을 수학적으로 보여준 것입니다.
또한 무베라의 변환 방법은 ColBERT뿐만 아니라 다른 다중 벡터 모델들에도 동일하게 적용할 수 있다는 점에서 모델 독립적(model-agnostic)입니다. 이는 새로운 모델이 등장해도 무베라의 효율성 개선 효과를 그대로 누릴 수 있음을 의미합니다. 무베라 적용의 개선 효과의 첫번째는 속도 개선효과입니다. 실험 결과에 따르면, 무베라를 적용했을 때 검색 정확도는 원본 방식의 95% 이상을 유지하면서도 검색 속도가 기존 다중 벡터 방식 대비 수십 배에서 수백 배까지 빨라짐을 확인할 수 있었습니다. 두번째는 확장성의 개선 효과입니다. 전통적인 다중 벡터 방식은 문서 수가 증가할수록 검색 시간이 기하급수적으로 늘어나지만, 무베라는 기존 단일 벡터 방식과 유사한 확장성을 보여줍니다.
무베라의 등장의 가장 큰 의의는 고성능 다중 벡터 검색 기술의 민주화의 가능성입니다. 이전에는 거대한 컴퓨팅 자원을 가진 대기업들만이 실용적으로 활용할 수 있었던 기술이, 이제는 중소 규모의 조직에서도 현실적으로 도입할 수 있게 되었다는 점이라고 생각합니다. 이러한 다중 벡터 검색 기술의 비용적 절감에 의한 민주화는 향후에 이 기술이 다양한 분야에 적용될 수 있을을 암시합니다. 실시간 개인화 추천, 대화형 검색 시스템, 멀티모달 검색 등이 다양한 부분에서 새로운 가능성이 열리게 될 것입니다.
